dimensional analysis problems with answers pdf
Dimensional analysis is a problem-solving technique focusing on the manipulation of dimensions and units․ It ensures consistency in equations, aiding in the derivation of formulas and verification of physical relationships․ Widely used in physics, chemistry, and engineering, it simplifies complex problems by breaking them into fundamental units․
Fundamental Principles of Dimensional Analysis
The core principle is dimensional homogeneity, ensuring all terms in an equation have consistent units․ This maintains physical meaning and validity, preventing errors in derivations and calculations․
Each physical quantity comprises magnitude and unit, adhering to fundamental dimensions like length, mass, and time․
Importance of Units in Dimensional Analysis
Units are the cornerstone of dimensional analysis, ensuring clarity and consistency in scientific and engineering calculations․ They provide a standardized way to express measurements, facilitating communication among researchers and practitioners․ Without consistent units, equations and relationships become ambiguous, leading to potential errors․ Units also play a critical role in verifying the dimensional homogeneity of equations, a fundamental principle of dimensional analysis․ By ensuring that all terms in an equation have compatible units, scientists can identify mistakes early in the problem-solving process․ Moreover, units help in simplifying complex problems by breaking them down into their fundamental components, such as length, mass, and time․ This systematic approach enhances accuracy and reduces the risk of miscalculations․ In essence, units are not just labels but essential tools that underpin the validity and reliability of dimensional analysis across diverse fields․
Dimensional Homogeneity: A Core Concept
Dimensional homogeneity is a foundational principle in dimensional analysis, ensuring that all terms in an equation are measurable in the same units․ This concept mandates that every term in an equation must have identical dimensions, allowing for valid mathematical operations․ For instance, adding quantities with differing dimensions, such as meters and kilograms, is fundamentally flawed․ Dimensional homogeneity serves as a powerful tool for validating the correctness of derived equations and identifying potential errors early in the problem-solving process․ It also aids in simplifying complex relationships by ensuring that all variables are expressed in consistent units․ By maintaining dimensional homogeneity, researchers and engineers can enhance the accuracy and reliability of their calculations․ This principle is particularly crucial in fields like physics and engineering, where precise measurements are essential․ In summary, dimensional homogeneity is not just a theoretical construct but a practical necessity that underpins the integrity of scientific and engineering analyses․

Practical Applications of Dimensional Analysis
Dimensional analysis is versatile and essential for identifying proportional relationships and verifying formulas․ It is widely applied in physics, chemistry, and engineering to solve problems involving unit conversions, formula derivations, and error detection, ensuring accurate and consistent results in practical scenarios․
Dimensional Analysis in Physics
In physics, dimensional analysis is a cornerstone for solving problems and verifying the consistency of equations․ It is used to derive formulas, such as Newton’s law of gravitation, by ensuring that all terms have compatible dimensions․ For example, in fluid dynamics, it helps determine the relationship between velocity, density, and viscosity․ By analyzing dimensions, physicists can identify essential variables and simplify complex systems․ Additionally, dimensional analysis aids in unit conversions, a critical skill in experimental physics․ It also helps detect errors in derivations by checking dimensional homogeneity․ Resources like “Dimensional Analysis Problems with Answers PDF” provide practice in applying these techniques to real-world scenarios․ These materials cover topics from basic mechanics to advanced electromagnetism, offering step-by-step solutions․ They are invaluable for students and professionals seeking to refine their problem-solving abilities․ Regular practice with such resources enhances one’s understanding of physical principles and their practical applications․
Dimensional Analysis in Chemistry
Dimensional analysis is a vital tool in chemistry, particularly in stoichiometry and unit conversions․ It ensures that chemical equations and calculations are dimensionally consistent, preventing errors in experiments and data interpretation․ For instance, when calculating molarity or converting between moles and grams, dimensional analysis helps maintain precision․ In gas law problems, it verifies that pressure, volume, and temperature are in compatible units․ This technique is also essential for solving problems involving chemical kinetics, where rate constants must have appropriate dimensions․ Resources like “Dimensional Analysis Problems with Answers PDF” provide exercises tailored to chemistry, covering topics such as concentration calculations, reaction rates, and thermodynamic quantities․ These materials often include step-by-step solutions, enabling learners to master complex calculations․ Regular practice with such resources enhances problem-solving skills and deepens the understanding of chemical principles․ By focusing on dimensional consistency, chemists can ensure the accuracy and reliability of their work, from laboratory experiments to theoretical models․
Dimensional Analysis in Engineering
Dimensional analysis plays a pivotal role in engineering, providing a systematic approach to solving design and operational problems․ Engineers use it to ensure consistency in units and dimensions across various formulas and equations, which is critical for accurate calculations․ For example, in fluid mechanics, dimensional analysis helps determine flow rates, pressure drops, and other parameters by maintaining consistent units․ In structural engineering, it ensures that stress and strain calculations adhere to fundamental physical laws․ Resources like “Dimensional Analysis Problems with Answers PDF” offer practice exercises tailored to engineering applications, covering topics such as beam analysis, thermodynamics, and materials science․ These materials often include real-world scenarios, allowing engineers to apply theoretical concepts to practical challenges․ By mastering dimensional analysis, engineers can minimize errors, optimize designs, and improve the safety and efficiency of their work․ Regular practice with these resources is essential for both students and professionals seeking to enhance their problem-solving skills in engineering․

Common Mistakes in Dimensional Analysis
One of the most frequent errors in dimensional analysis is ignoring the physical significance of dimensions, leading to invalid equations․ Many learners mistakenly combine unrelated quantities or fail to convert units properly, resulting in inconsistent results․ Another common oversight is neglecting to account for all fundamental dimensions, such as mass, length, and time, which are essential for maintaining dimensional homogeneity; Additionally, some individuals misapply formulas or assume dimensional equivalence where it does not exist, leading to incorrect conclusions․ These mistakes often stem from a lack of attention to unit consistency or a misunderstanding of the underlying principles․ Practicing with resources like “Dimensional Analysis Problems with Answers PDF” can help identify and correct these errors․ By addressing these pitfalls, learners can improve their ability to apply dimensional analysis effectively in various scientific and engineering contexts․
Tips for Solving Dimensional Analysis Problems
Mastering dimensional analysis requires a systematic approach and attention to detail․ Start by clearly defining the units of all quantities involved to ensure consistency․ Always check for dimensional homogeneity in equations, as this is a fundamental principle․ Break down complex problems into smaller, manageable steps to avoid confusion․ When converting units, use conversion factors appropriately and verify each step to prevent errors․ Practicing with resources like “Dimensional Analysis Problems with Answers PDF” can help refine your skills․ Pay special attention to the cancellation of units, as this often reveals whether the solution is on the right track․ Additionally, avoid mixing unrelated dimensions, such as combining time and length without proper context․ Regularly reviewing common mistakes and learning from them is essential for improvement․ By following these tips, learners can enhance their problem-solving efficiency and accuracy in dimensional analysis․
Resources for Practicing Dimensional Analysis
Access “Dimensional Analysis Problems with Answers PDF” for comprehensive practice․ Utilize online platforms like Khan Academy and Coursera for additional resources․ Worksheets and practice exams are also available to refine your skills in dimensional analysis effectively․
Best PDF Materials for Practice
For effective practice, “Dimensional Analysis Problems with Answers PDF” offers comprehensive exercises and solutions․ These materials cover various fields, from basic physics to advanced engineering applications․ They are ideal for students and professionals seeking to master unit conversion and dimensional homogeneity․
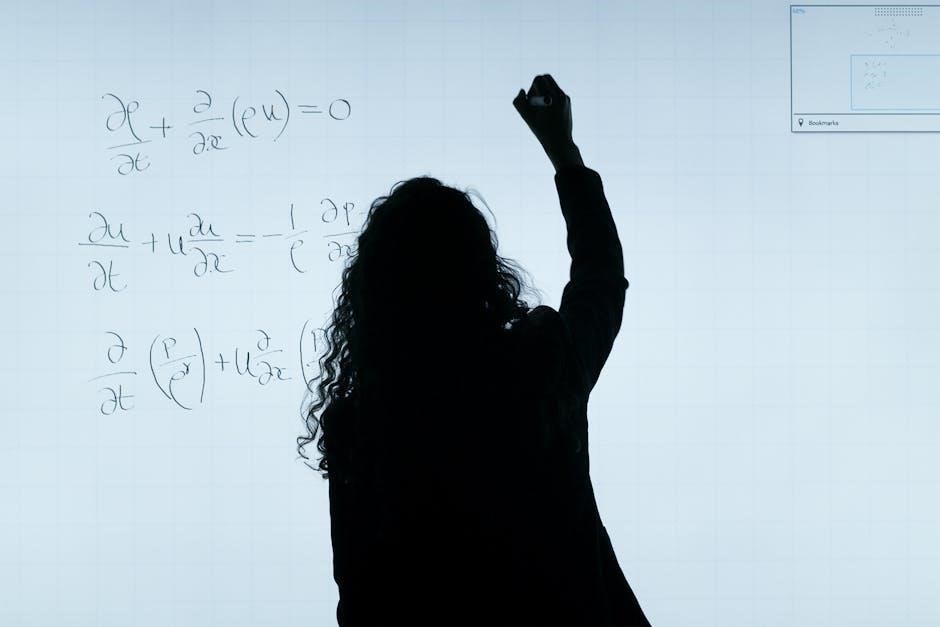
Many PDF resources include worked-out examples, allowing learners to follow problem-solving steps closely․ They often feature multiple-choice questions and detailed explanations, making self-assessment easier; Additionally, these materials are designed to align with standard curricula, ensuring relevance and depth․
Some recommended PDFs focus on specific areas, such as chemistry or physics, while others provide general dimensional analysis exercises․ Websites like educational portals and online libraries offer free downloads․ Platforms like Coursera and Khan Academy also provide supplementary PDF materials for practice․
Regular practice with these PDFs helps build proficiency in handling complex problems․ Start with basic exercises to grasp fundamentals, then progress to advanced questions․ This structured approach ensures a solid understanding of dimensional analysis․
Online Platforms for Additional Problems
Several online platforms offer additional dimensional analysis problems with answers, catering to diverse learning needs․ Websites like Coursera and Khan Academy provide free resources, including video tutorials and practice sheets․ These platforms often include interactive tools for solving problems step-by-step․
Other popular sites, such as Quizlet and Chegg, offer detailed problem sets with solutions․ They cover topics ranging from basic unit conversions to complex engineering applications․ Some platforms also feature forums where users can discuss challenges and share tips․
For advanced learners, platforms like Brilliant and MIT OpenCourseWare offer specialized problems in physics and chemistry․ These resources are ideal for those seeking to deepen their understanding of dimensional analysis․ Regular practice on these platforms ensures mastery of the subject․
Learners can track their progress and identify areas needing improvement․ Many platforms provide timed quizzes to simulate exam conditions, enhancing problem-solving speed and accuracy․ Utilizing these online resources complements traditional study materials effectively․
Start with basic exercises to build a strong foundation, then gradually move to more complex problems․ This approach ensures a comprehensive understanding of dimensional analysis, making it easier to tackle real-world applications․
Dimensional analysis is a cornerstone in science and engineering, ensuring consistency in equations and verifying physical relationships․ By focusing on units and dimensions, it simplifies complex problems, making them more manageable․ This technique is versatile, aiding in derivations, unit conversions, and validating formulas across physics, chemistry, and engineering․
Regular practice with resources like dimensional analysis problems with answers PDF helps build proficiency․ These materials provide structured exercises, from basic unit manipulations to advanced applications, reinforcing understanding․ Solving problems consistently improves problem-solving speed and accuracy, essential for academic and professional success․

Dimensional analysis fosters a deeper understanding of physical phenomena, enabling professionals to tackle real-world challenges effectively․ It is not just a mathematical tool but a foundational skill that enhances analytical thinking and precision․ Mastering it is crucial for excelling in STEM fields, where accuracy and logical reasoning are paramount․

